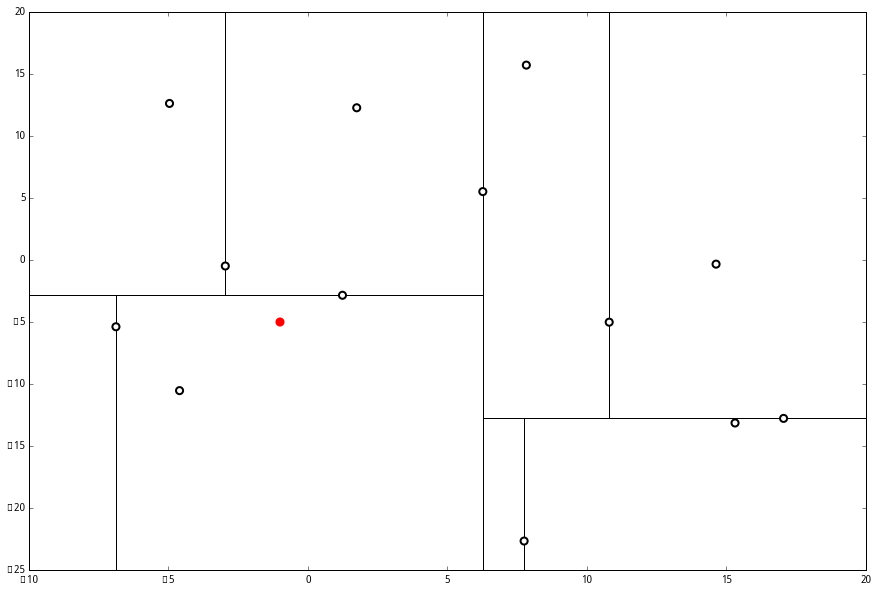
分布式向量检索

实际上就是一个knn的模型

[!tip] KNN 如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别

kdtree

用于快速检索最近的k个点

kdtree

[!tip] 参考 https://www.joinquant.com/view/community/detail/c2c41c79657cebf8cd871b44ce4f5d97

结构
```
struct kdtree{
    Node-data // 数据矢量   数据集中某个数据点，是n维矢量（这里也就是k维）
    Range     // 空间矢量   该节点所代表的空间范围
    split     // 整数       垂直于分割超平面的方向轴序号
    Left      //  kd树       由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
    Right     // kd树       由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
    parent    // kd树       父节点
}
```
- 实际上有点类似Mysql底层原理 > 联合索引,首先选取第一个坐标(这个点中位数最好,不是的话左右两边点数量会有影响),将所有数据大于这个的放在左边,小于这个的放置在右边,建立类似二叉树
- 然后选择第二个坐标,如法炮制,直到所有坐标都放进去
查找过程
1. 设 L 为一个有 k 个空位的列表，用于保存已搜寻到的最近点
2. 根据 p 的坐标值和每个节点的切分向下搜索,根据第一个属性比较
3. 当达到一个底部节点(这里是必须是最底下的节点)时，将其标记为访问过。如果 L 里不足 k 个点，则将当前节点的特征坐标加入 L ；如果 L 不为空并且当前节点的特征与 p 的距离小于 L 里最长的距离，则用当前特征替换掉 L 中离 p 最远的点
4. 如果当前节点是整棵树最顶端节点,算法完成,如果不是
  - 向上爬一个节点。如果当前（向上爬之后的）节点未曾被访问过，将其标记为被访问过，然后执行下面的1和2；如果当前节点被访问过，再次向上爬
    1. 如果此时 L 里不足 k 个点，则将节点特征加入 L；如L 中已满 k个点，且当前节点与 p 的距离小于 L 里最长的距离,则用节点特征替换掉 L 中离最远的点
    2. 计算 p 和当前节点切分线的距离。如果该距离大于等于 L 中距离 p 最远的距离并且 L 中已有 k 个点，则在切分线另一边不会有更近的点，执行(三)；如果该距离小于 L 中最远的距离或者 L 中不足 k个点，则切分线另一边可能有更近的点，因此在当前节点的另一个枝从(1)开始执行.这一步是核心:如果比中线分割线的距离都比目前所有的远就不用找另外一边了,==注意不是中间的点,是中间的分割线,这才是最短距离==

缺点

对于高维数据不友好,未读高了之后大量数据在边界,使得分割效果不好
对于数据分布敏感,如果出现数据集分布不均的问题很容易导致树高低不平影响查询效率,包括后续的添加也会影响高度
添加数据之后维护非常麻烦

局部敏感哈希

可以参考 GitHub - facebookresearch/faiss: A library for efficient similarity search and clustering of dense vectors.

欧式空间中，将高维空间的点映射到低维空间，原本接近的点在低维空间中肯定依然接近，但原本远离的点则有一定概率变成接近的点。

选取多个合适的哈希函数,将向量哈希化后放入结果的bukket中
相识寻找的时候直接将找多个bukket的and 或者or(看业务需要,大部分是直接and)

核心方法是用空间换取时间,计算非常简单
缺点
1. 并不是完全精确,很可能出现错漏的情况
2. 和hash函数关联性强,数据量和会影响整体的效果,数据量大用小桶+and,数据量小用大桶+or

点数越多，我们越应该增加每个分桶函数中桶的个数；相反，点数越少，我们越应该减少桶的个数；
Embedding 向量的维度越大，我们越应该增加哈希函数的数量，尽量采用且的方式作为多桶策略；相反，Embedding 向量维度越小，我们越应该减少哈希函数的数量，多采用或的方式作为分桶策略。

Grose

服务的节点只负责提供api和先数据库中写入反馈之类的
worker负责计算用户最喜欢的物品然后写入数据库中
master负责收集信息并指挥worker干活

参考

https://nxwz51a5wp.feishu.cn/docs/doccnsvpGMaaLfmOu1LAmorDH4b
https://gorse.io/zh/docs/

chenxuan'blog