跳表
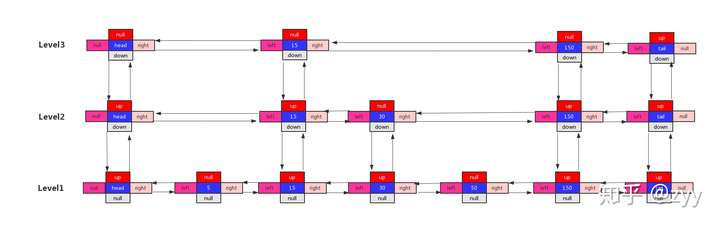
- 就是一个二维链表,从有序链表构建
- 最上层开始查,下一个比他小就向右,否则向下
- 插入数据后random,50%的概率向上插入,递归向上遍历
优缺点
- 实现简单,比平衡树简单多了
- 比B树占用内存更少
- 缓存局部性
确定层数
- level=log2(n) - 1,每一层是下一层的一半
洗牌算法
步骤
- 将数组分为以弄混和为弄混两部分
- 随机从未弄混(包含自己)拿出一个和未弄混的最后一个位置进行调换

- 标记最后一个为已弄混

- 重复步骤
Top K算法
步骤
- 底层是快排,时间复杂度是O(n)
- 使用快排方法,拿到pos,判断pos和k关系
- 在len比k大的区间进行递归,直到找到pos正好为k时候
如果使用堆的方法,插入n个元素的时间复杂度为O(n log n),取出前K个元素的时间复杂度为O(K log n),因此,总的时间复杂度为O(n log n + K log n),即O((n + K) log n) 快速选择算法实现取出最大K个元素的时间复杂度为O(n),其中n为优先队列中的元素个数。快速选择算法的时间复杂度与快速排序类似,平均情况下为O(n),最坏情况下为O(n^2)
P和NP问题
P类问题
- 多项式时间(Polynomial time)
- 能用经典计算机轻易解决的所有问题
- P类中的算法必须在n^c的时间内停止并给出正确答案,其中n是输入的规模,c是常数
如某个数是否为质数
NP类问题
- 不确定多项式时间 (Non-deterministic Polynomial time)
- 能用经典计算机快速验证答案的所有问题
- 如果给出某问题一个答案,存在对答案正确性的简短的证明,那么该问题就是一个NP问题
有没有一个公式能推出下一个质数是多少呢?这种问题的答案,是无法直接计算得到的,只能通过间接的“猜算”来得到结果。这也就是非确定性问题。而这些问题的通常有个算法,它不能直接告诉你答案是什么,但可以告诉你,某个可能的结果是正确的答案还是错误的。这个可以告诉你“猜算”的答案正确与否的算法,假如可以在多项式(polynomial)时间内算出来,就叫做多项式非确定性问题。 生成问题的一个解通常比验证一个给定的解时间花费要多得多,如果某人告诉你,数13,717,421可以写成两个较小的数的乘积,你可能不知道是否应该相信他,但是如果他告诉你他可以因式分解为3607乘上3803,那么你就可以用一个袖珍计算器容易验证这是对的
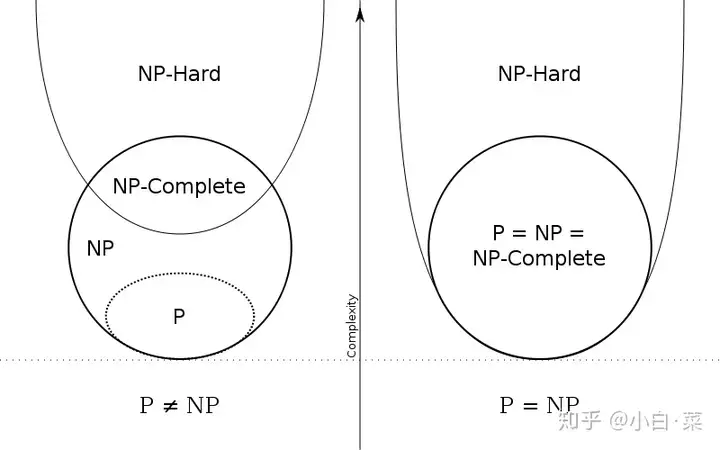
P=NP?
- P 问题和 NP 问题是否等价。如果 P = NP 就意味着任何能够在多项式的复杂度验证的问题也能够在多项式的复杂度解决它
- 如果p=np,RSA加密将会在多项式时间内攻破,意味着加密算法是不安全的,O(x^k),k为一个常数(目前最先进也是指数级).同时意味着所有问题都可以用计算机解决了
线段树
- 通过一个数组管辖的区域不同,每个数组元素代表一个区域的和
参考
- https://zhuanlan.zhihu.com/p/144002143
- https://zhuanlan.zhihu.com/p/141884913
- https://baike.baidu.com/item/NP%E5%AE%8C%E5%85%A8%E9%97%AE%E9%A2%98/4934286
- https://zhuanlan.zhihu.com/p/260083265

