55. 跳跃游戏

给定一个非负整数数组 `nums` ，你最初位于数组的 **第一个下标** 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。

DFS,深度优先,遍历所有可能的路径(太慢)
贪心,维护一个最远可到达地点,然后最后比较是否是终点就ok

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size();
        int rightmost = 0;
        for (int i = 0; i < n; ++i) {
            if (i <= rightmost) {
                rightmost = max(rightmost, i + nums[i]);
                if (rightmost >= n - 1) {
                    return true;
                }
            }
        }
        return false;
    }
};

64. 最小路径和

给定一个包含非负整数的 `_m_ x _n_` 网格 `grid` ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步。

典型的BFS

200. 岛屿数量

给你一个由 `'1'`（陆地）和 `'0'`（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

经典BFS或者并查集

207. 课程表

你这个学期必须选修 `numCourses` 门课程，记为 `0` 到 `numCourses - 1` 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 `prerequisites` 给出，其中 `prerequisites[i] = [ai, bi]` ，表示如果要学习课程 `ai` 则 **必须** 先学习课程  `bi` 。

-   例如，先修课程对 `[0, 1]` 表示：想要学习课程 `0` ，你需要先完成课程 `1` 。

请你判断是否可能完成所有课程的学习？如果可以，返回 `true` ；否则，返回 `false` 。

有向图是否存在环的问题
DFS或者BFS

215. 数组中的第K个最大元素

给定整数数组 `nums` 和整数 `k`，请返回数组中第 `**k**` 个最大的元素。
请注意，你需要找的是数组排序后的第 `k` 个最大的元素，而不是第 `k` 个不同的元素。
你必须设计并实现时间复杂度为 `O(n)` 的算法解决此问题。

TOPK

2290. 到达角落需要移除障碍物的最小数目

给你一个下标从 **0** 开始的二维整数数组 `grid` ，数组大小为 `m x n` 。每个单元格都是两个值之一：
-   `0` 表示一个 **空** 单元格，
-   `1` 表示一个可以移除的 **障碍物** 。
你可以向上、下、左、右移动，从一个空单元格移动到另一个空单元格。
现在你需要从左上角 `(0, 0)` 移动到右下角 `(m - 1, n - 1)` ，返回需要移除的障碍物的 **最小** 数目。

本质上是BFS,遍历中加入下次可以走的点,如果通过这条路到达下一个点的代价小于之前遍历的这个点的代价,将这个点加入队列中继续遍历
巧妙地一点在于障碍物看作代价为1的点,然后找到代价最小的点

class Solution {
    static constexpr int dirs[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
public:
    int minimumObstacles(vector<vector<int>> &grid) {
        int m = grid.size(), n = grid[0].size();
        int dis[m][n];
        memset(dis, 0x3f, sizeof(dis));
        dis[0][0] = 0;
        deque<pair<int, int>> q;
        q.emplace_front(0, 0);
        while (!q.empty()) {
            auto [x, y] = q.front();
            q.pop_front();
            for (auto &[dx, dy] : dirs) {
                int nx = x + dx, ny = y + dy;
                if (0 <= nx && nx < m && 0 <= ny && ny < n) {
                    int g = grid[nx][ny];
                    if (dis[x][y] + g < dis[nx][ny]) {
                        dis[nx][ny] = dis[x][y] + g;
                        g == 0 ? q.emplace_front(nx, ny) : q.emplace_back(nx, ny);
                    }
                }
            }
        }
        return dis[m - 1][n - 1];
    }
};

其他

BFS和DFS邻接矩阵时候时间复杂度为O(n2)

寻路算法

BFS和DFS

BFS主要用于最短路径,但是比较慢需要全图遍历
DFS主要用于解决有没有路径的问题

Dijkstra 算法

计算每一个节点距离起点的总移动代价。同时，还需要一个优先队列结构。对于所有待遍历的节点，放入优先队列中会按照代价进行排序.这个代价通常是到这里需要消耗的距离或者步数,每次都从优先队列中选出代价最小的作为下一个遍历的节点。直到到达终点为止。
如果这个代价设置为每个节点到达终点的距离作为优先级，每次始终选取到终点移动代价最小（离终点最近）的节点作为下一个遍历的节点。这种算法称之为最佳优先（Best First）算法。

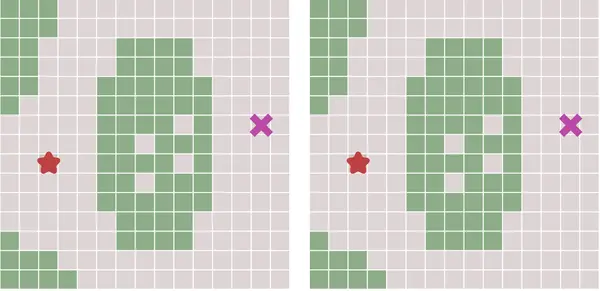
A*算法

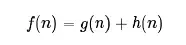
通过两个函数(g和h)结果得到优先级,然后放到优先队列中,每次找优先级最高的遍历
f(n)是节点n的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（值最小）的节点。
g(n) 是节点n距离起点的代价。
h(n)是节点n距离终点的预计代价，也就是A*算法的启发函数

* 初始化open_set和close_set；
* 将起点加入open_set中，并设置优先级为0（优先级最高）；
* 如果open_set不为空，则从open_set中选取优先级最高的节点n：
    * 如果节点n为终点，则：
        * 从终点开始逐步追踪parent节点，一直达到起点；
        * 返回找到的结果路径，算法结束；
    * 如果节点n不是终点，则：
        * 将节点n从open_set中删除，并加入close_set中；
        * 遍历节点n所有的邻近节点：
            * 如果邻近节点m在close_set中，则：
                * 跳过，选取下一个邻近节点
            * 如果邻近节点m也不在open_set中，则：
                * 设置节点m的parent为节点n
                * 计算节点m的优先级
                * 将节点m加入open_set中

[!tip] h(n)启发函数

在极端情况下，当启发函数h(n)始终为0，则将由g(n)决定节点的优先级，此时算法就退化成了Dijkstra算法。

如果h(n)始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。

如果h(n)完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。

如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。

在另外一个极端情况下，如果h(n)相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

如果图形中只允许朝上下左右四个方向移动，则可以使用曼哈顿距离（Manhattan distance）。

如果图形中允许朝八个方向移动，则可以使用对角距离。

如果图形中允许朝任何方向移动，则可以使用欧几里得距离（Euclidean distance）。

实际上来说 h(n)相当于深度优先,g(n)相当于广度优先,这两个权重的大小决定了结果和过程

[!tip] 参考路径规划之 A* 算法 - 知乎

参考

https://zhuanlan.zhihu.com/p/54510444

chenxuan'blog