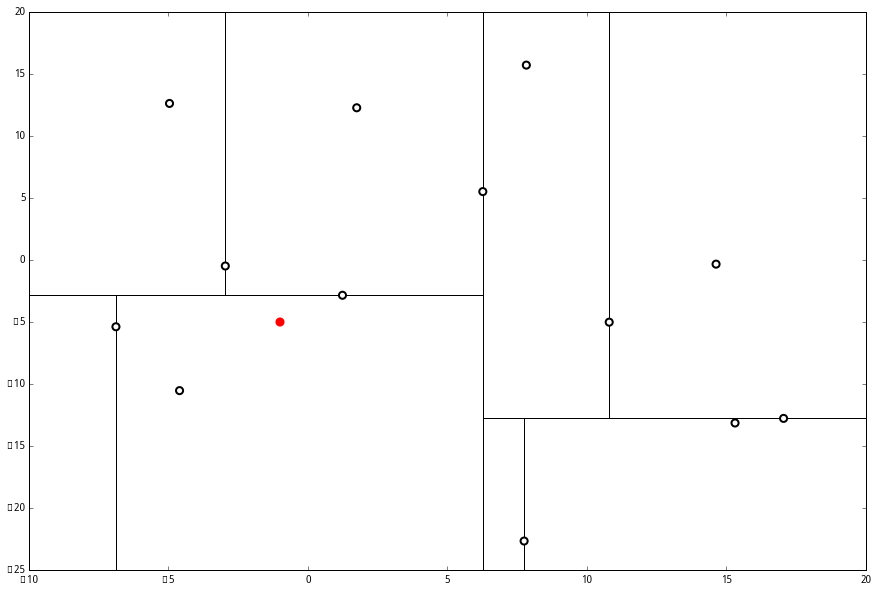
105. 从前序与中序遍历序列构造二叉树
239. 滑动窗口最大值
给你一个整数数组 `nums`,有一个大小为 `k` 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 `k` 个数字。滑动窗口每次只向右移动一位。
返回 _滑动窗口中的最大值_ 。
- 优先队列,堆,不着急删除,拿出来检查是否删除,删除继续拿
297. 二叉树的序列化与反序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
**提示:** 输入输出格式与 LeetCode 目前使用的方式一致,详情请参阅 [LeetCode 序列化二叉树的格式](https://leetcode.cn/faq/#binary-tree)。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
- 通过加上NULL,变成完全二叉树再进行遍历就OK
295. 数据流的中位数
**中位数**是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
- 例如 `arr = [2,3,4]` 的中位数是 `3` 。
- 例如 `arr = [2,3]` 的中位数是 `(2 + 3) / 2 = 2.5` 。
实现 MedianFinder 类:
- `MedianFinder()` 初始化 `MedianFinder` 对象。
- `void addNum(int num)` 将数据流中的整数 `num` 添加到数据结构中。
- `double findMedian()` 返回到目前为止所有元素的中位数。与实际答案相差 `10-5` 以内的答案将被接受。
- 思路非常惊奇,使用两个优先队列,每次加数字判断放到哪一边的优先队列,然后查询直接从头部查询就ok
class MedianFinder {
public:
priority_queue<int, vector<int>, less<int>> queMin;
priority_queue<int, vector<int>, greater<int>> queMax;
MedianFinder() {}
void addNum(int num) {
if (queMin.empty() || num <= queMin.top()) {
queMin.push(num);
if (queMax.size() + 1 < queMin.size()) {
queMax.push(queMin.top());
queMin.pop();
}
} else {
queMax.push(num);
if (queMax.size() > queMin.size()) {
queMin.push(queMax.top());
queMax.pop();
}
}
}
double findMedian() {
if (queMin.size() > queMax.size()) {
return queMin.top();
}
return (queMin.top() + queMax.top()) / 2.0;
}
};
哈夫曼编码
[!tip] 参考 https://zhuanlan.zhihu.com/p/144562146
- 本质是根据每个char出现的频率不同进行的优化压缩编码
- 如e的频率最高,z频率低,但是都是占用一个char大小,就会非常浪费
- 如果把e用0一个位表示,z用1111111标识,大小就会压缩
- 必须满足只用两个符号(即0和1)和前缀不重复这两个特征

生成过程
- 统计文本中字符出现的次数
- 将字符按照频数升序排序
- 将频数最小的两个叶子结点结合成树,看作一个整体,整体的频数是叶子结点频数和
- 把这个树看作整体和其他的一起也进行升序排序
- 重复上述过程知道生成整棵树
// 哈夫曼树节点定义
struct HuffmanNode {
char c;
int freq;
HuffmanNode* left;
HuffmanNode* right;
HuffmanNode(char cc = '\0', int f = 0, HuffmanNode* l = nullptr, HuffmanNode* r = nullptr) :
c(cc), freq(f), left(l), right(r) {}
};
// 哈夫曼树构建函数
HuffmanNode* buildHuffmanTree(unordered_map<char, int>& freqMap) {
auto cmp = [](HuffmanNode* a, HuffmanNode* b) {
return a->freq > b->freq;
};
priority_queue<HuffmanNode*, vector<HuffmanNode*>, decltype(cmp)> q(cmp); // 小根堆
for (auto& p : freqMap) {
q.push(new HuffmanNode(p.first, p.second));
}
while (q.size() > 1) {
auto leftNode = q.top(); q.pop();
auto rightNode = q.top(); q.pop();
auto parent = new HuffmanNode('\0', leftNode->freq + rightNode->freq, leftNode, rightNode);
q.push(parent);
}
return q.top();
}
// 递归构建 Huffman 编码表
void buildHuffmanCodeTable(HuffmanNode* node, string code, unordered_map<char, string>& codeTable) {
if (!node) return;
if (node->c != '\0') {
codeTable[node->c] = code;
}
buildHuffmanCodeTable(node->left, code + '0', codeTable);
buildHuffmanCodeTable(node->right, code + '1', codeTable);
}
Morris遍历
- Morris一种遍历二叉树的方式,并且时间复杂度为O(N),额外空间复杂度O(1)
- 实质就是利用叶节点具有大量空指针,通过这些空指针连成原本需要的栈达到目的
- 如果遍历要求不能改变树的结构,那么不能用这个Morris遍历
void morrisPreorder(TreeNode* root) {
TreeNode *cur = root, *pre = NULL;
while (cur != NULL) {
if (cur->left == NULL) {
cout << cur->val << " ";
cur = cur->right;
} else {
pre = cur->left;
while (pre->right != NULL && pre->right != cur)
pre = pre->right;
if (pre->right == NULL) {
cout << cur->val << " ";
pre->right = cur;
cur = cur->left;
} else {
pre->right = NULL;
cur = cur->right;
}
}
}
}
502. IPO
假设 力扣(LeetCode)即将开始 **IPO** 。为了以更高的价格将股票卖给风险投资公司,力扣 希望在 IPO 之前开展一些项目以增加其资本。 由于资源有限,它只能在 IPO 之前完成最多 `k` 个不同的项目。帮助 力扣 设计完成最多 `k` 个不同项目后得到最大总资本的方式。
给你 `n` 个项目。对于每个项目 `i` ,它都有一个纯利润 `profits[i]` ,和启动该项目需要的最小资本 `capital[i]` 。
最初,你的资本为 `w` 。当你完成一个项目时,你将获得纯利润,且利润将被添加到你的总资本中。
总而言之,从给定项目中选择 **最多** `k` 个不同项目的列表,以 **最大化最终资本** ,并输出最终可获得的最多资本。
答案保证在 32 位有符号整数范围内。
- 著名的银行家算法(用于避免死锁)
- 利用堆的贪心算法
- 项目按照所需资本的从小到大进行排序,每次进行选择时,假设当前手中持有的资本为 w,我们应该从所有投入资本小于等于 w 的项目中选择利润最大的项目 j,然后此时我们更新手中持有的资本为
w+profits[j],同时再从所有花费资本小于等于 w+profits[j]的项目中选择,我们按照上述规则不断选择 k 次即可 - 利用大根堆的特性,我们将所有能够投资的项目的利润全部压入到堆中,每次从堆中取出最大值,然后更新手中持有的资本,同时将待选的项目利润进入堆,不断重复上述操作。
- 项目按照所需资本的从小到大进行排序,每次进行选择时,假设当前手中持有的资本为 w,我们应该从所有投入资本小于等于 w 的项目中选择利润最大的项目 j,然后此时我们更新手中持有的资本为
typedef pair<int,int> pii;
class Solution {
public:
int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {
int n = profits.size();
int curr = 0;
priority_queue<int, vector<int>, less<int>> pq;
vector<pii> arr;
for (int i = 0; i < n; ++i) {
arr.push_back({capital[i], profits[i]});
}
sort(arr.begin(), arr.end());
for (int i = 0; i < k; ++i) {
while (curr < n && arr[curr].first <= w) {
pq.push(arr[curr].second);
curr++;
}
if (!pq.empty()) {
w += pq.top();
pq.pop();
} else {
break;
}
}
return w;
}
};
632. 最小区间
你有 `k` 个 **非递减排列** 的整数列表。找到一个 **最小** 区间,使得 `k` 个列表中的每个列表至少有一个数包含在其中。
我们定义如果 `b-a < d-c` 或者在 `b-a == d-c` 时 `a < c`,则区间 `[a,b]` 比 `[c,d]` 小。
- 每个数组维护一个指针,标识现在是哪一个位置.通过堆维护所有指针中数据最小的
class Solution {
public:
vector<int> smallestRange(vector<vector<int>>& nums) {
vector<int> points(nums.size(),0);
pair<int, int> result={-1,-1},minNow=result;
auto cmp = [](pair<int, int>& a, pair<int, int>& b) {
return a.first > b.first;
};
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> que(cmp);
for (int i = 0; i < nums.size(); i++) {
que.push({nums[i][points[i]],i});
minNow.second=max(minNow.second,nums[i][points[i]]);
}
while (!que.empty()) {
auto now=que.top();
que.pop();
minNow.first=now.first;
if (result.first==-1||minNow.second-minNow.first<result.second-result.first) {
result=minNow;
}
points[now.second]++;
auto pos=points[now.second];
if (pos==nums[now.second].size()) {
break;
}
minNow.second=max(minNow.second,nums[now.second][pos]);
que.push({nums[now.second][pos],now.second});
}
return vector<int>()={result.first,result.second};
}
}
树状数组
- 是线段树的一种
- 非常单纯,就是用来求
单点修改,区间查询的情况的 - #算法技巧
- 当出现区间修改,单点查询的时候,使用的是差分数组
- 不修改,只区间查询使用前缀和
- 只有单点修改,区间查询时候才使用树状数组
作用
- 可以用于求区间和,最简单的做法
- 用于于求逆序对
- 将数组离散化,即建立连续的对应关系,算出多少个不同的数字为n,将原来数组的元素一一映射到1-n
- 遍历数组,遇到数字求比他小的数组和(详细步骤可见1694题)
class Bit{//树状数组,作用是`单点改变,区间区和`
public:
Bit(int size){//设置bit数组长度,index需要小于这个
tree.resize(size+1,0);
}
private:
vector<int> tree;
int lowBit(int x) {
return x & (-x);
}
public:
void add(int index, int val) {//将某个index的val加上给定值
index+=1;
while (index < (int)tree.size()) {
tree[index] += val;
index += lowBit(index);
}
}
int prefixSum(int index) {//将数组的下标为0-index的数字求和,**包括自己**
index+=1;
int sum = 0;
while (index > 0) {
sum += tree[index];
index -= lowBit(index);
}
return sum;
}
};
找到数组中第一个比某个元素大的元素使用单调栈,统计比某个元素大的元素有多少个使用树状数组
完全二叉树的扁平化
- 完全二叉树除了最下面那一层,其他层都是满的,二叉堆都是完全二叉树
- 参考

2179. 统计数组中好三元组数目
给你两个下标从 **0** 开始且长度为 `n` 的整数数组 `nums1` 和 `nums2` ,两者都是 `[0, 1, ..., n - 1]` 的 **排列** 。
**好三元组** 指的是 `3` 个 **互不相同** 的值,且它们在数组 `nums1` 和 `nums2` 中出现顺序保持一致。换句话说,如果我们将 `pos1v` 记为值 `v` 在 `nums1` 中出现的位置,`pos2v` 为值 `v` 在 `nums2` 中的位置,那么一个好三元组定义为 `0 <= x, y, z <= n - 1` ,且 `pos1x < pos1y < pos1z` 和 `pos2x < pos2y < pos2z` 都成立的 `(x, y, z)` 。
请你返回好三元组的 **总数目** 。
- 典型的树状数组,惊艳的是三元组,使用中间的数为分界线,而不是左右两边,遇到3个的题可以参考
long long goodTriplets(vector<int>& nums1, vector<int>& nums2){
long long result=0;
unordered_map<int,int> hashmap;
int len=nums1.size();
for(unsigned i=0;i<nums2.size();i++)
hashmap.insert(pair<int,int>{nums2[i],i});
for(unsigned i=0;i<nums1.size();i++)
nums1[i]=hashmap[nums1[i]];
Bit pre(len),after(len);
vector<int> arrleft(len,0),arrright(len,0);
for (int i = 0; i < len; i++) {
arrleft[i]=pre.prefixSum(nums1[i]);
pre.add(nums1[i], 1);
}
for (int i = len-1; i>=0; i--) {
arrright[i]=after.prefixSum(len-1)-after.prefixSum(nums1[i]);
after.add(nums1[i], 1);
}
for (int i = 0; i < len; i++) {
result+=arrleft[i]*(long long)arrright[i];
}
return result;
}
金山wps笔试第二题
大概是两只队伍挑人,一个数组,依次选目前分数最高的人,和左右的各m个人,输出整个队伍最后的情况
数量级是10^5
- 首先使用构建堆,每次从堆那人出来,维护unorderset,记录是否有队伍,同时维护一个双向链表(vector pair)维护每个人的上一个和下一个人,每次动态更新,挺复杂的,用到了挺多数据结构的
各种树
满二叉树
- 只有最后一层的节点没有子节点,其他都是满的
二叉搜索树

- 左边比父节点小,右边比父节大,高度无限制
AVL树(平衡二叉树)
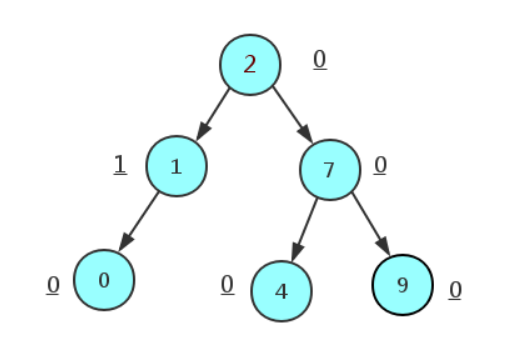
- 左右子树高度差不超过1,其他满足二叉搜索树的特点
红黑树

- 每个节点非红即黑.
- 根节点是黑的。
- 每个叶节点(叶节点即树尾端NUL指针或NULL节点)都是黑的.
- 如果一个节点是红的,那么它的两儿子都是黑的.
- 对于任意节点而言,其到叶子点树NIL指针的每条路径都包含相同数目的黑节点.
B-tree
没有B-树,只有B树
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束(节点中存储真实数据);
- 其搜索性能等价于在关键字全集内做一次二分查找;
- 自动层次控制;
B+tree
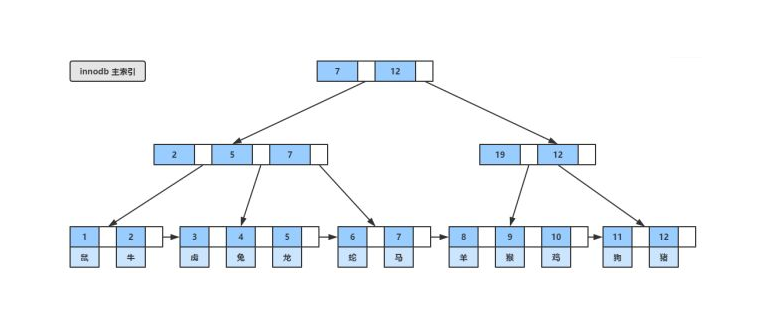
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的
- 不可能在非叶子结点命中
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
- 更适合文件索引系统
trie tree(前缀树)
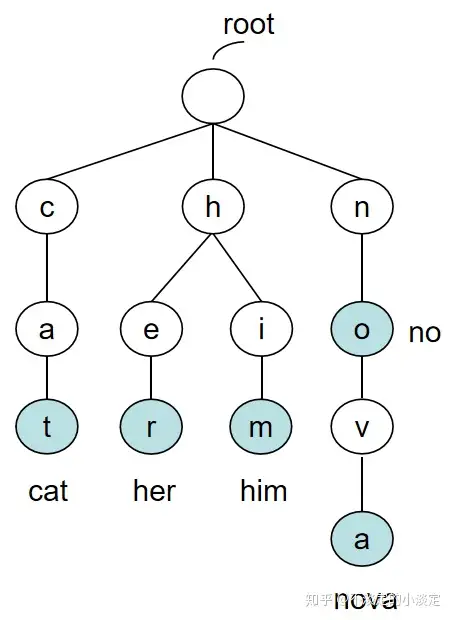
- 又称为前缀树,常用于根据前缀快速搜索匹配(比如ip域的匹配)
radix tree
[!tip] 参考 https://www.zhihu.com/question/41961814/answer/2685709494 https://zhuanlan.zhihu.com/p/644667990
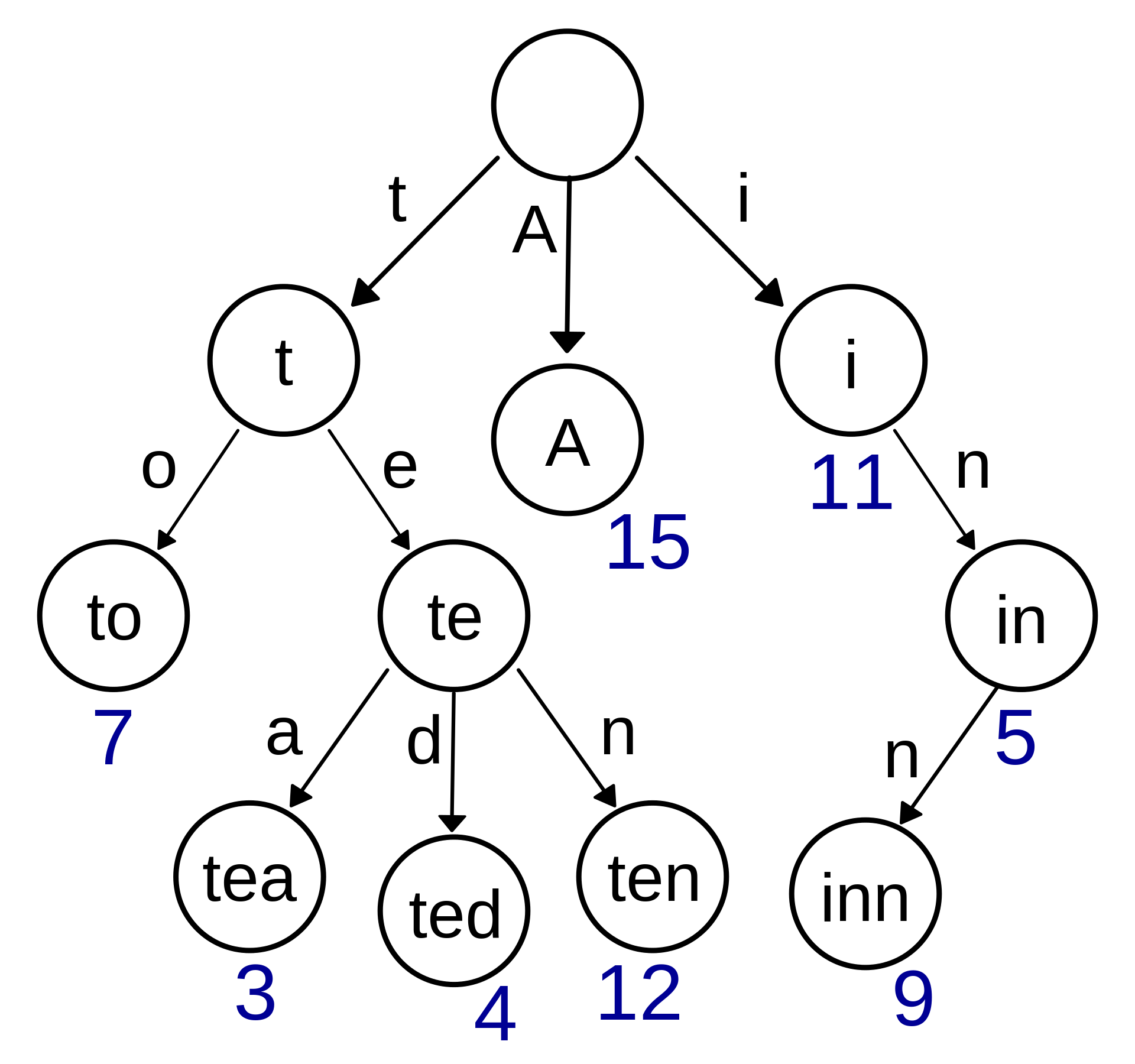
- 实际上就是一个节点的key不是单一的一个字符,可能存在多个字符的情况
- 实际上就是一种特殊的前缀树(Trie tree)
结构体
typedef struct raxNode {
uint32_t iskey:1; //节点是否包含key
uint32_t isnull:1; //节点的值是否为NULL
uint32_t iscompr:1; //节点是否被压缩
uint32_t size:29; //节点大小
unsigned char data[]; //节点的实际存储数据
} raxNode;
- #TODO 这部分后面根据参考补全一下
kdtree
[!tip] 参考 https://www.joinquant.com/view/community/detail/c2c41c79657cebf8cd871b44ce4f5d97
结构
struct kdtree{
Node-data // 数据矢量 数据集中某个数据点,是n维矢量(这里也就是k维)
Range // 空间矢量 该节点所代表的空间范围
split // 整数 垂直于分割超平面的方向轴序号
Left // kd树 由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
Right // kd树 由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
parent // kd树 父节点
}
- 实际上有点类似Mysql底层原理 > 联合索引,首先选取第一个坐标(这个点中位数最好,不是的话左右两边点数量会有影响),将所有数据大于这个的放在左边,小于这个的放置在右边,建立类似二叉树
- 然后选择第二个坐标,如法炮制,直到所有坐标都放进去
查找过程
- 设 L 为一个有 k 个空位的列表,用于保存已搜寻到的最近点
- 根据 p 的坐标值和每个节点的切分向下搜索,根据第一个属性比较
- 当达到一个底部节点(这里是必须是最底下的节点)时,将其标记为访问过。如果 L 里不足 k 个点,则将当前节点的特征坐标加入 L ;如果 L 不为空并且当前节点的特征与 p 的距离小于 L 里最长的距离,则用当前特征替换掉 L 中离 p 最远的点
- 如果当前节点是整棵树最顶端节点,算法完成,如果不是
- 向上爬一个节点。如果当前(向上爬之后的)节点未曾被访问过,将其标记为被访问过,然后执行 下面的1和2;如果当前节点被访问过,再次向上爬
- 如果此时 L 里不足 k 个点,则将节点特征加入 L;如L 中已满 k个点,且当前节点与 p 的距离小于 L 里最长的距离,则用节点特征替换掉 L 中离最远的点
- 计算 p 和当前节点切分线的距离。如果该距离大于等于 L 中距离 p 最远的距离并且 L 中已有 k 个点,则在切分线另一边不会有更近的点,执行(三);如果该距离小于 L 中最远的距离或者 L 中不足 k个点,则切分线另一边可能有更近的点,因此在当前节点的另一个枝从(1)开始执行.这一步是核心:如果比中线分割线的距离都比目前所有的远就不用找另外一边了,==注意不是中间的点,是中间的分割线,这才是最短距离==
- 向上爬一个节点。如果当前(向上爬之后的)节点未曾被访问过,将其标记为被访问过,然后执行 下面的1和2;如果当前节点被访问过,再次向上爬