原理
- 本质就是穷举法+记忆化
- https://labuladong.gitee.io/algo/di-er-zhan-a01c6/dong-tai-g-a223e/dong-tai-g-1e688/
# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):
for 选择 in 所有可能的选择:
# 此时的状态已经因为做了选择而改变
result = 求最值(result, dp(状态1, 状态2, ...))
return result
# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 求最值(选择1,选择2...)
5. 最长回文子串
给你一个字符串 `s`,找到 `s` 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
- 动态规划经典,用 P(i,j)P(i,j) 表示字符串 s的第 i到 j个字母组成的串(下文表示成 s[i:j])是否为回文串,P(i,j)=P(i+1,j−1)∧(Si==Sj)
53. 最大子数组和
给你一个整数数组 `nums` ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
**子数组** 是数组中的一个连续部分。
- 经典简单dp,选择自己或者上一个加上自己中大的那个
class Solution {
public:
int maxSubArray(vector<int>& nums) {
if(nums.size()==0){
return 0;
}
int result=nums[0];
for(unsigned i=1;i<nums.size();i++){
nums[i]=max(nums[i-1]+nums[i],nums[i]);
result=max(result,nums[i]);
}
return result;
}
};
升级版最大子数组和(小红书笔试)
给你一个整数数组 `nums` 和一个数字`change`,**你最多可以将数组中一个数修改成change**,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
**子数组** 是数组中的一个连续部分。
- 加了一个条件最多可以修改一个数字,变成了类似股票的问题,dp分为现在没用过这次机会和用过了这次机会,没用这次机会和最大子数组和类似,用了的是max(max(之前用过+原来数字,之前没用+change),change),实际上就是之前用还是当前用,当前用需要比较加上之前没用的最大值
vector<pair<long long,long long>> dp(size,{0,0});
long long result=0;
for (int j = 0; j < size; j++) {
if (j==0) {
dp[j].first=arr[j];
dp[j].second=change;
result=max(dp[j].first,dp[j].second);
continue;
}
dp[j].first=max(dp[j-1].first+arr[j],arr[j]);
dp[j].second=max(max(dp[j-1].first+change,dp[j-1].second+arr[j]),change);
result=max(result,max(dp[j].first,dp[j].second));
}
72. 编辑距离
给你两个单词 `word1` 和 `word2`, _请返回将 `word1` 转换成 `word2` 所使用的最少操作数_ 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
- 超经典动态规划
- dp[i][j]表示 s1[0..i] 和 s2[0..j] 的最小编辑距离

class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.length();
int m = word2.length();
if (n * m == 0) return n + m;
vector<vector<int>> D(n + 1, vector<int>(m + 1));
for (int i = 0; i < n + 1; i++) {
D[i][0] = i;
}
for (int j = 0; j < m + 1; j++) {
D[0][j] = j;
}
// 计算所有 DP 值
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < m + 1; j++) {
int left = D[i - 1][j] + 1;
int down = D[i][j - 1] + 1;
int left_down = D[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1]) left_down += 1;
D[i][j] = min(left, min(down, left_down));
}
}
return D[n][m];
}
};
198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,**如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警**。
给定一个代表每个房屋存放金额的非负整数数组,计算你 **不触动警报装置的情况下** ,一夜之内能够偷窃到的最高金额。
- 简单动态规划
dp[i]=max(dp[i−2]+nums[i],dp[i−1])
322. 零钱兑换
给你一个整数数组 `coins` ,表示不同面额的硬币;以及一个整数 `amount` ,表示总金额。
计算并返回可以凑成总金额所需的 **最少的硬币个数** 。如果没有任何一种硬币组合能组成总金额,返回 `-1` 。
你可以认为每种硬币的数量是无限的。
- 经典动态规划
vector<int> dp(amount+1,-1);
for (int i=1; i<=amount; i++) {
for (auto& coin : coins) {
if (coin==i) {
dp[i]=1;
}else if (coin<i&&dp[i-coin]!=-1) {
if (dp[i]!=-1) {
dp[i]=min(dp[i],dp[i-coin]+1);
}else {
dp[i]=dp[i-coin]+1;
}
}
}
}
139. 单词拆分
给你一个字符串 `s` 和一个字符串列表 `wordDict` 作为字典。请你判断是否可以利用字典中出现的单词拼接出 `s` 。
**注意:**不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
dp[i]表示字符串s的[0,i)(当i==0时表示空串) 的字母组成的单词能否由字典中的单词拼接而成- 状态转移的时候,考虑枚举分割点
j (0 <= j <= i), 将字符串分成[0,j)和[j,i)两部分, 注意j==0时,第一部分是空串,j==i时,第二部分是空串 - 如果两部分都在字典中,则整个串可以由字典中的单词拼成
- 因为计算到
dp[i]的时候,已经计算出了dp[0]....dp[i-1]的值, 所以[0,j)直接由dp[j]即可得到 - 所以只需计算
[j,i)在不在字典中即可 - 所以如果
[j,i)在字典中且dp[j]为true, 则dp[i] = true, 否则dp[i] = false
func wordBreak(s string, wordDict []string) bool {
n := len(s)
dp := make([]bool, n+1)
// set 快速判断字符串在不在字典中
set := make(map[string]struct{})
for _, word := range wordDict {
set[word] = struct{}{}
}
dp[0] = true // 空串一定能被拼出来
for i := 1; i <= n; i++ {
// 枚举分割点 j
for j := 0; j <= i; j++ {
if _, ok := set[s[j:i]]; dp[j] && ok {
dp[i] = true
break
}
}
}
return dp[n]
}
152. 乘积最大子数组
给你一个整数数组 `nums` ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 **32-位** 整数。
**子数组** 是数组的连续子序列。
- 分为正数和负数分别进行dp
1035. 不相交的线
在两条独立的水平线上按给定的顺序写下 `nums1` 和 `nums2` 中的整数。
现在,可以绘制一些连接两个数字 `nums1[i]` 和 `nums2[j]` 的直线,这些直线需要同时满足满足:
- `nums1[i] == nums2[j]`
- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
- 底层是最长公共子序列
class Solution {
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>> dp(nums1.size(),vector<int>(nums2.size(),0));
for (int i = 0; i < nums1.size(); i++) {
for (int j = 0; j < nums2.size(); j++) {
if(nums1[i]==nums2[j]){
if(i>0&&j>0){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=1;
}
}else {
if (i>0&&j>0) {
dp[i][j]=max(dp[i][j-1],max(dp[i-1][j],dp[i-1][j-1]));
}else if(i==0&&j==0){
dp[i][j]=0;
}else if (i==0) {
dp[i][j]=dp[i][j-1];
}else if (j==0){
dp[i][j]=dp[i-1][j];
}
}
if(i==nums1.size()-1&&j==nums2.size()-1){
return dp[i][j];
}
}
}
return 0;
}
};
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 `stones` 表示。其中 `stones[i]` 表示第 `i` 块石头的重量。
每一回合,从中选出**任意两块石头**,然后将它们一起粉碎。假设石头的重量分别为 `x` 和 `y`,且 `x <= y`。那么粉碎的可能结果如下:
- 如果 `x == y`,那么两块石头都会被完全粉碎;
- 如果 `x != y`,那么重量为 `x` 的石头将会完全粉碎,而重量为 `y` 的石头新重量为 `y-x`。
最后,**最多只会剩下一块** 石头。返回此石头 **最小的可能重量** 。如果没有石头剩下,就返回 `0`。
- #TODO 补全这部分
class Solution {
public:
int lastStoneWeightII(vector<int> &stones) {
int sum = accumulate(stones.begin(), stones.end(), 0);
int m = sum / 2;
vector<int> dp(m + 1);
dp[0] = true;
for (int weight : stones) {
for (int j = m; j >= weight; --j) {
dp[j] = dp[j] || dp[j - weight];
}
}
for (int j = m;; --j) {
if (dp[j]) {
return sum - 2 * j;
}
}
}
};
1043. 分隔数组以得到最大和
给你一个整数数组 `arr`,请你将该数组分隔为长度 **最多** 为 k 的一些(连续)子数组。分隔完成后,每个子数组的中的所有值都会变为该子数组中的最大值。
返回将数组分隔变换后能够得到的元素最大和。本题所用到的测试用例会确保答案是一个 32 位整数。
- 典型dp,向前查找k个内的值的最大值
class Solution {
public:
int maxSumAfterPartitioning(vector<int>& arr, int k) {
vector<int> dp(arr.size(),0);
for (int i = 0; i < arr.size(); i++) {
int now=arr[i],maxNow=arr[i];
if (i!=0) {
now+=dp[i-1];
}
for (int j=i-1; j>=0&&j>i-k; j--) {
maxNow=max(maxNow,arr[j]);
if (j!=0) {
now=max(now,maxNow*(i-j+1)+dp[j-1]);
}else {
now=max(now,maxNow*(i+1));
}
}
dp[i]=now;
}
return dp[dp.size()-1];
}
};
354. 俄罗斯套娃信封问题
给你一个二维整数数组 `envelopes` ,其中 `envelopes[i] = [wi, hi]` ,表示第 `i` 个信封的宽度和高度。
当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算 **最多能有多少个** 信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
**注意**:不允许旋转信封。
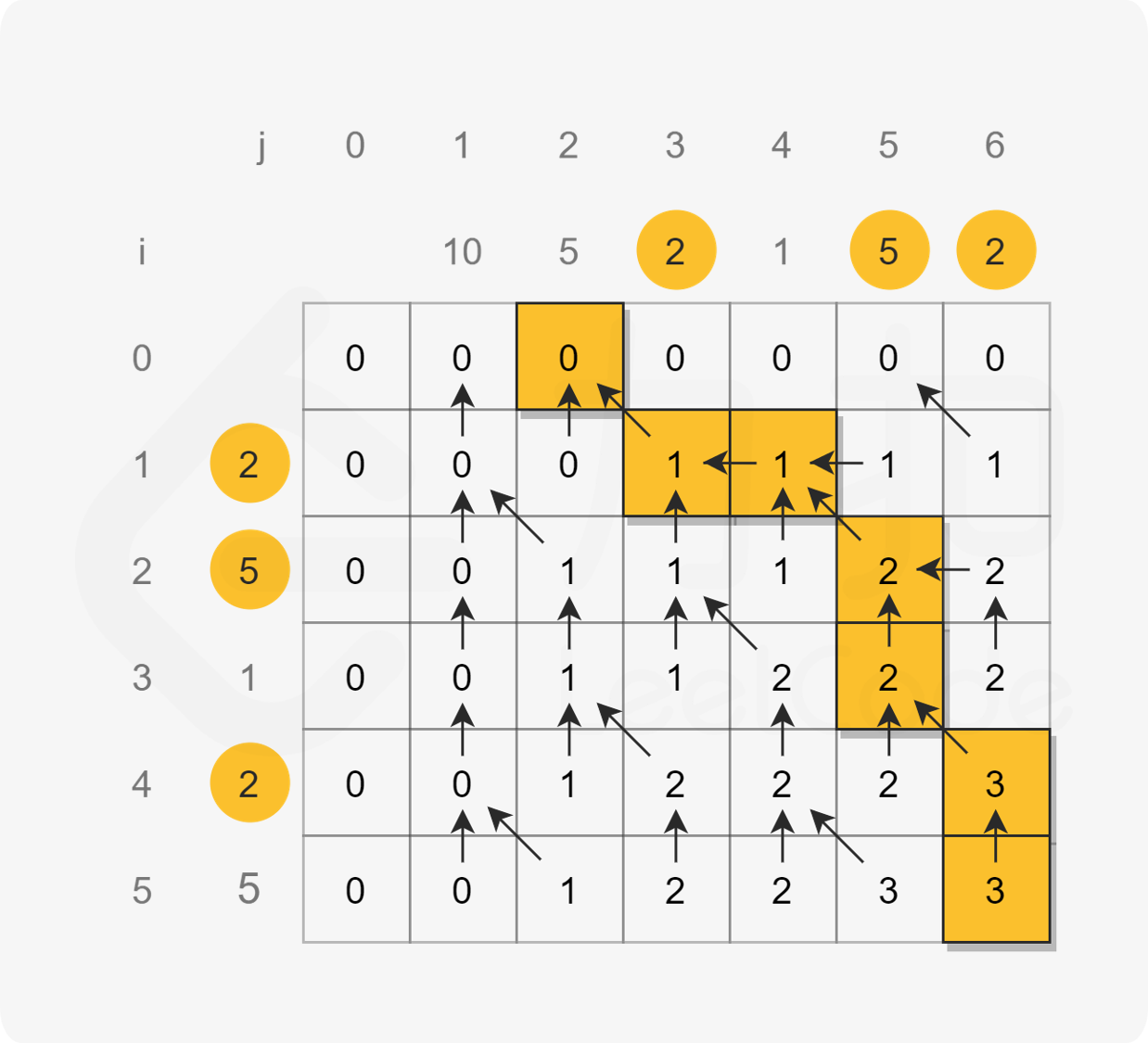
- 首先经过一轮排序根据x的值正序,y的值逆序(逆序的原因是保证每一个相同的w只能选择一个),然后根据y的值寻找最长递增子序列
- 寻找最长递增子序列的方法也是动态规划
如排序成(1,3),(1,1),(2,6),(2,4),(3,7),(3,1)
class Solution {
public:
int maxEnvelopes(vector<vector<int>>& envelopes) {
if (envelopes.empty()) {
return 0;
}
int n = envelopes.size();
sort(envelopes.begin(), envelopes.end(), [](const auto& e1, const auto& e2) {
return e1[0] < e2[0] || (e1[0] == e2[0] && e1[1] > e2[1]);
});
vector<int> f(n, 1);
for (int i = 1; i < n; ++i) {
for (int j = 0; j < i; ++j) {
if (envelopes[j][1] < envelopes[i][1]) {
f[i] = max(f[i], f[j] + 1);
}
}
}
return *max_element(f.begin(), f.end());
}
};
264. 丑数 II
给你一个整数 `n` ,请你找出并返回第 `n` 个 **丑数** 。
**丑数** 就是只包含质因数 `2`、`3` 和/或 `5` 的正整数。
- 动态规划,因为下一个大的数字一定是有之前的数字乘于2,3,5得到,维护2,3,5三个指针,相当于使用2,3,5分别乘以之前出现的每一个数字,但是不是马上生成,而是每次比较下一个哪一个最小再移动,本质也是遍历,但是不需要提前计算很多数字,因为每次计算都是下一个最小的
class Solution {
public:
int nthUglyNumber(int n) {
vector<int> dp(n + 1);
dp[1] = 1;
int p2 = 1, p3 = 1, p5 = 1;
for (int i = 2; i <= n; i++) {
int num2 = dp[p2] * 2, num3 = dp[p3] * 3, num5 = dp[p5] * 5;
dp[i] = min(min(num2, num3), num5);
if (dp[i] == num2) {
p2++;
}
if (dp[i] == num3) {
p3++;
}
if (dp[i] == num5) {
p5++;
}
}
return dp[n];
}
};
174. 地下城游戏
恶魔们抓住了公主并将她关在了地下城 `dungeon` 的 **右下角** 。地下城是由 `m x n` 个房间组成的二维网格。我们英勇的骑士最初被安置在 **左上角** 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为_负整数_,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 _0_),要么包含增加骑士健康点数的魔法球(若房间里的值为_正整数_,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 **向右** 或 **向下** 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
**注意:**任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间
- 非常惊艳的题目,因为正向dp需要考虑剩余血量和走到当前位置的最少初始血量,导致无法dp,因此需要逆向dp,从终点向回走,因为从终点走,不需要考虑死亡的问题
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int n = dungeon.size(), m = dungeon[0].size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1, INT_MAX));
dp[n][m - 1] = dp[n - 1][m] = 1;
for (int i = n - 1; i >= 0; --i) {
for (int j = m - 1; j >= 0; --j) {
int minn = min(dp[i + 1][j], dp[i][j + 1]);
dp[i][j] = max(minn - dungeon[i][j], 1);
}
}
return dp[0][0];
}
};
410. 分割数组的最大值
给定一个非负整数数组 `nums` 和一个整数 `m` ,你需要将这个数组分成 `m` 个非空的连续子数组。
设计一个算法使得这 `m` 个子数组各自和的最大值最小。
- 这个中分割类的题型的同一解法可以令 发[i][j]表示将数组的前 i 个数分割为 j 段所能得到的最大连续子数组和的最小值。在进行状态转移时,我们可以考虑第 j 段的具体范围,即我们可以枚举 k,其中前 k 个数被分割为 j-1 段,而第 k+1 到第 i 个数为第 j 段。此时,这 j 段子数组中和的最大值,就等于 f[k][j−1] 与 sub(k+1,i)的较大值,其中 sub(i,j)表示数组 nums中下标落在区间 [i,j] 内的数的和。由于我们要使得子数组中和的最大值最小,因此可以列出如下的状态转移方程:
f[i][j]=min(0<=k<=i){max(f[k][j-1],sub(k+1,j))}
class Solution {
public:
int splitArray(vector<int>& nums, int m) {
int n = nums.size();
vector<vector<long long>> f(n + 1, vector<long long>(m + 1, LLONG_MAX));
vector<long long> sub(n + 1, 0);
for (int i = 0; i < n; i++) {
sub[i + 1] = sub[i] + nums[i];
}
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= min(i, m); j++) {
for (int k = 0; k < i; k++) {
f[i][j] = min(f[i][j], max(f[k][j - 1], sub[i] - sub[k]));
}
}
}
return (int)f[n][m];
}
};
- 贪心+二分法, #TODO 整理
2209. 用地毯覆盖后的最少白色砖块
给你一个下标从 **0** 开始的 **二进制** 字符串 `floor` ,它表示地板上砖块的颜色。
- `floor[i] = '0'` 表示地板上第 `i` 块砖块的颜色是 **黑色** 。
- `floor[i] = '1'` 表示地板上第 `i` 块砖块的颜色是 **白色** 。
同时给你 `numCarpets` 和 `carpetLen` 。你有 `numCarpets` 条 **黑色** 的地毯,每一条 **黑色** 的地毯长度都为 `carpetLen` 块砖块。请你使用这些地毯去覆盖砖块,使得未被覆盖的剩余 **白色** 砖块的数目 **最小** 。地毯相互之间可以覆盖。
请你返回没被覆盖的白色砖块的 **最少** 数目。
- 一个非常典型的动态规划问题类似背包问题,dp[i][j]标识第i块砖上放j块毛毯最大的覆盖面积
for (int i = 0; i < floor.size(); i++) {
if (i-carpetLen>=0) {
if (floor[i-carpetLen]=='1') {
now--;
}
}
if (floor[i]=='1') {
now++;
}
arr[i]=now;
}
vector<vector<int>> dp(floor.size(),vector<int>(numCarpets,0));
int all=0,cover=0;
for (int i = 0; i < floor.size(); i++) {
if (i>0) {
dp[i]=dp[i-1];
}
if (floor[i]=='1') {
all++;
int pos=i-carpetLen;
for (int j = 0; j < numCarpets; j++) {
int temp=0;
if (pos>=0&&j>0) {
temp=dp[pos][j-1];
}
dp[i][j]=max(dp[i][j],temp+arr[i]);
cover=max(cover,dp[i][j]);
}
}
}
return all-cover;
}
2998. 使 X 和 Y 相等的最少操作次数
给你两个正整数 `x` 和 `y` 。
一次操作中,你可以执行以下四种操作之一:
1. 如果 `x` 是 `11` 的倍数,将 `x` 除以 `11` 。
2. 如果 `x` 是 `5` 的倍数,将 `x` 除以 `5` 。
3. 将 `x` 减 `1` 。
4. 将 `x` 加 `1` 。
请你返回让 `x` 和 `y` 相等的 **最少** 操作次数。
- 一个很有意思的dp题目,因为不是先往常的可以从前向后遍历(类似青蛙跳那种),这个状态从前和后面都出现了
- 因此这里需要引入bfs
queue<int> que;
que.push(x);
while (!que.empty()) {
auto pos=que.front();
auto num=dp[pos];
que.pop();
if (pos%11==0&&num+1<dp[pos/11]) {
dp[pos/11]=num+1;
que.push(pos/11);
}
if (pos%5==0&&num+1<dp[pos/5]) {
dp[pos/5]=num+1;
que.push(pos/5);
}
if (pos>0&&num+1<dp[pos-1]) {
dp[pos-1]=num+1;
que.push(pos-1);
}
if (pos+1<dp.size()&&num+1<dp[pos+1]) {
dp[pos+1]=num+1;
que.push(pos+1);
}
}
360笔试第二题
用1表示a,用2表示b...,26标识z,给定一个字符串(如1324929067),求这个字符串能对应多少种ab这种类型的标识
- 用的是dp优点难想到,这种一般想到的是递归
- 使用dp[i]表示前i个数字有多少种表示,根据dp[i-1]和dp[i-2]获取
int last=-1;
for (int i = 0; i < size; i++) {
int now=str[i]-'0';
int old=now;
if (now==0) {
if (last==-1||last==0) {
cout<<0;
return 0;
}else {
now=last*10+now;
if(now>26||i<1){
cout<<0;
return 0;
}
if (i>1) {
dp[i]+=dp[i-2]%mod;
}else {
dp[i]=1;
}
}
}else {
if (i!=0) {
dp[i]+=dp[i-1]%mod;
}else {
dp[i]+=1;
}
if (last>0) {
now=last*10+now;
if (now<=26) {
if (i>1) {
dp[i]+=dp[i-2]%mod;
}else {
dp[i]+=1;
}
}
}
}
dp[i]%=mod;
last=old;
}
区间dp
- 将数组分成若干份,求每份某个属性之和的最值就可以想到“I型区间DP”,套路很固定
1335. 工作计划的最低难度
你需要制定一份 `d` 天的工作计划表。工作之间存在依赖,要想执行第 `i` 项工作,你必须完成全部 `j` 项工作( `0 <= j < i`)。
你每天 **至少** 需要完成一项任务。工作计划的总难度是这 `d` 天每一天的难度之和,而一天的工作难度是当天应该完成工作的最大难度。
给你一个整数数组 `jobDifficulty` 和一个整数 `d`,分别代表工作难度和需要计划的天数。第 `i` 项工作的难度是 `jobDifficulty[i]`。
返回整个工作计划的 **最小难度** 。如果无法制定工作计划,则返回 **-1** 。
- 直接看这里
class Solution {
public:
int minDifficulty(vector<int>& jobDifficulty, int d) {
int n = jobDifficulty.size();
if (n < d) {
return -1;
}
vector<vector<int>> dp(d + 1, vector<int>(n, 0x3f3f3f3f));
int ma = 0;
for (int i = 0; i < n; ++i) {
ma = max(ma, jobDifficulty[i]);
dp[0][i] = ma;
}
for (int i = 1; i < d; ++i) {
for (int j = i; j < n; ++j) {
ma = 0;
for (int k = j; k >= i; --k) {
ma = max(ma, jobDifficulty[k]);
dp[i][j] = min(dp[i][j], ma + dp[i - 1][k - 1]);
}
}
}
return dp[d - 1][n - 1];
}
};
股票问题
121. 买卖股票的最佳时机
给定一个数组 `prices` ,它的第 `i` 个元素 `prices[i]` 表示一支给定股票第 `i` 天的价格。
你只能选择 **某一天** 买入这只股票,并选择在 **未来的某一个不同的日子** 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 `0` 。
- 作为easy,只需要记下目前最小值作为买入,遍历时候顺便计算利润最大值
122. 买卖股票的最佳时机 II
给你一个整数数组 `prices` ,其中 `prices[i]` 表示某支股票第 `i` 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 **最多** 只能持有 **一股** 股票。你也可以先购买,然后在 **同一天** 出售。
返回 _你能获得的 **最大** 利润_
- 贪心:收集所有上坡的部分,结果一定最大化
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
int n = prices.size();
for (int i = 1; i < n; ++i) {
ans += max(0, prices[i] - prices[i - 1]);
}
return ans;
}
};
- 动态规划
- 定义状态 dp[i][0]表示第 i 天交易完后手里没有股票的最大利润,dp[i][1]表示第 i天交易完后手里持有一支股票的最大利润(i 从 0 开始)
dp[i][0]=max{dp[i−1][0],dp[i−1][1]+prices[i]}
dp[i][1]=max{dp[i−1][1],dp[i−1][0]−prices[i]}
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int dp0 = 0, dp1 = -prices[0];
for (int i = 1; i < n; ++i) {
int newDp0 = max(dp0, dp1 + prices[i]);
int newDp1 = max(dp1, dp0 - prices[i]);
dp0 = newDp0;
dp1 = newDp1;
}
return dp0;
}
};
714. 买卖股票的最佳时机含手续费
给定一个整数数组 `prices`,其中 `prices[i]`表示第 `i` 天的股票价格 ;整数 `fee` 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
**注意:**这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
- 类似上一题,只不过购买的时候加上手续费
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2));
dp[0][0] = 0, dp[0][1] = -prices[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
};
- 类似上一题的贪心算法,判断时候需要大于手续费
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
int buy = prices[0] + fee;
int profit = 0;
for (int i = 1; i < n; ++i) {
if (prices[i] + fee < buy) {
buy = prices[i] + fee;
}
else if (prices[i] > buy) {
profit += prices[i] - buy;
buy = prices[i];
}
}
return profit;
}
};
309. 最佳买卖股票时机含冷冻期
给定一个整数数组`prices`,其中第 `prices[i]` 表示第 `_i_` 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 也是动态规划,不过dp[i][1]从上上个获取
class Solution {
public:
int maxProfit(vector<int>& prices) {
vector<vector<int>> value(prices.size(),vector<int>(2,0));
value[0][0]=0,value[0][1]=-prices[0];
for(unsigned i=1;i<prices.size();i++)
{
value[i][0]=max(value[i-1][0],value[i-1][1]+prices[i]);
if(i>1)
value[i][1]=max(value[i-1][1],value[i-2][0]-prices[i]);
else
value[i][1]=max(value[i-1][1],value[i-1][0]-prices[i]);
}
return value[value.size()-1][0];
}
};
123. 买卖股票的最佳时机 III IV
给定一个数组,它的第 `i` 个元素是一支给定的股票在第 `i` 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 **两笔** 交易。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 由于我们最多可以完成两笔交易,因此在任意一天结束之后,我们会处于以下五个状态中的一种: 未进行过任何操作; 只进行过一次买操作; 进行了一次买操作和一次卖操作,即完成了一笔交易; 在完成了一笔交易的前提下,进行了第二次买操作; 完成了全部两笔交易。
for (int i = 0; i < prices.size(); i++) {
if (i==0) {
dp[i][0]=0;
dp[i][1]=-prices[0];
}else {
auto& last=dp[i-1];
dp[i][0]=last[0];
dp[i][1]=max(last[0]-prices[i],last[1]);
if (i>0) {
dp[i][2]=max(last[1]+prices[i],last[2]);
}
if (i>1) {
dp[i][3]=max(last[2]-prices[i],last[3]);
}
if (i>2) {
dp[i][4]=max(last[3]+prices[i],last[4]);
}
}
auto iter=max_element(dp[i].begin(),dp[i].end());
result=max(result,*iter);
}
打劫问题
198. 打家劫舍I and III
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,**如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警**。
给定一个代表每个房屋存放金额的非负整数数组,计算你 **不触动警报装置的情况下** ,一夜之内能够偷窃到的最高金额。
- 简单动态规划问题,核心在于两个状态的dp
dp[0]=nums[0]只有一间房屋,则偷窃该房屋
dp[1]=max(nums[0],nums[1])只有两间房屋,选择其中金额较高的房屋进行偷窃
213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 **围成一圈** ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,**如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警** 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 **在不触动警报装置的情况下** ,今晚能够偷窃到的最高金额。
- 上面类似,分两种情况,偷第一家,删除最后一家,不偷第一家,从1开始遍历
背包问题
01背包问题
有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。**每件物品只能用一次**,求解将哪些物品装入背包里物品价值总和最大。
- dp[i][j]的含义:从下标[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
- 由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]
- 由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
- 所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]
// 初始化:第一列都是0,第一行表示只选取0号物品最大价值
for (int j = bagWeight; j >= weight[0]; j--)
dp[0][j] = dp[0][j - weight[0]] + value[0];
// weight数组的大小 就是物品个数
for (int i = 1; i < weight.size(); i++) // 遍历物品(第0个物品已经初始化)
{
for (int j = 0; j <= bagWeight; j++) // 遍历背包容量
{
if (j < weight[i]) //背包容量已经不足以拿第i个物品了
dp[i][j] = dp[i - 1][j]; //最大价值就是拿第i-1个物品的最大价值
//背包容量足够拿第i个物品,可拿可不拿:拿了最大价值是前i-1个物品扣除第i个物品的 重量的最大价值加上i个物品的价值
//不拿就是前i-1个物品的最大价值,两者进行比较取较大的
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
- 二维代码可以进行优化,去除选取物品的那一层,简化为一维背包 // 一维 //状态定义:dp[j]表示容量为j的背包能放下东西的最大价值
// 初始化
vector<int> dp(bagWeight + 1, 0);
for (int i = 0; i < weight.size(); i++)
{ // 遍历物品
for (int j = bagWeight; j >= weight[i]; j--)
{ // 遍历背包容量(一定要逆序)
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); //不取或者取第i个
}
}
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 `stones` 表示。其中 `stones[i]` 表示第 `i` 块石头的重量。
每一回合,从中选出**任意两块石头**,然后将它们一起粉碎。假设石头的重量分别为 `x` 和 `y`,且 `x <= y`。那么粉碎的可能结果如下:
- 如果 `x == y`,那么两块石头都会被完全粉碎;
- 如果 `x != y`,那么重量为 `x` 的石头将会完全粉碎,而重量为 `y` 的石头新重量为 `y-x`。
最后,**最多只会剩下一块** 石头。返回此石头 **最小的可能重量** 。如果没有石头剩下,就返回 `0`。
- 从一堆石头中,每次拿两块重量分别为x,y的石头,若x=y,则两块石头均粉碎;若x<y,两块石头变为一块重量为y-x的石头求最后剩下石头的最小重量(若没有剩下返回0) 问题转化为:把一堆石头分成两堆,求两堆石头重量差最小值 进一步分析:要让差值小,两堆石头的重量都要接近sum/2;我们假设两堆分别为A,B,A<sum/2,B>sum/2,若A更接近sum/2,B也相应更接近sum/2 进一步转化:将一堆stone放进最大容量为sum/2的背包,求放进去的石头的最大重量MaxWeight,最终答案即为sum-2*MaxWeight
参考
- https://zhuanlan.zhihu.com/p/345364527
- https://leetcode.cn/problems/last-stone-weight-ii/solutions/805162/yi-pian-wen-zhang-chi-tou-bei-bao-wen-ti-5lfv/