146. LRU 缓存
请你设计并实现一个满足 [LRU (最近最少使用) 缓存](https://baike.baidu.com/item/LRU) 约束的数据结构。
实现 `LRUCache` 类:
`LRUCache(int capacity)` 以 **正整数** 作为容量 `capacity` 初始化 LRU 缓存
`int get(int key)` 如果关键字 `key` 存在于缓存中,则返回关键字的值,否则返回 `-1` 。
`void put(int key, int value)` 如果关键字 `key` 已经存在,则变更其数据值 `value` ;如果不存在,则向缓存中插入该组 `key-value` 。如果插入操作导致关键字数量超过 `capacity` ,则应该 **逐出** 最久未使用的关键字。
函数 `get` 和 `put` 必须以 `O(1)` 的平均时间复杂度运行。
- 通过双向链表,最新使用的插入链表头,删除链表内原来地址,淘汰链表尾部分
- 通过map建立key和node*之间联系.
[!question] 缺点 对突发流量表现差,突然的大量key很可能把一些重要的key踢下去
[!quote] 场景 如果数据的使用频率比较均匀,没有明显的热点数据,那么 LRU 算法比较适合。例如,一个在线书店的图书搜索页面,用户搜索图书的请求会比较频繁,但是对于每本书的访问并没有特别的频繁,这时 LRU 算法就能够很好地满足需求。
460. LFU 缓存
请你为 [最不经常使用(LFU)](https://baike.baidu.com/item/%E7%BC%93%E5%AD%98%E7%AE%97%E6%B3%95)缓存算法设计并实现数据结构。
实现 `LFUCache` 类:
- `LFUCache(int capacity)` - 用数据结构的容量 `capacity` 初始化对象
- `int get(int key)` - 如果键 `key` 存在于缓存中,则获取键的值,否则返回 `-1` 。
- `void put(int key, int value)` - 如果键 `key` 已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量 `capacity` 时,则应该在插入新项之前,移除最不经常使用的项。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 **最近最久未使用** 的键。
为了确定最不常使用的键,可以为缓存中的每个键维护一个 **使用计数器** 。使用计数最小的键是最久未使用的键。
当一个键首次插入到缓存中时,它的使用计数器被设置为 `1` (由于 put 操作)。对缓存中的键执行 `get` 或 `put` 操作,使用计数器的值将会递增。
函数 `get` 和 `put` 必须以 `O(1)` 的平均时间复杂度运行。
- 通过有序map记录每一条key的使用频率,自动排序,用hash记录key和val关系,时间复杂度log(n)
- 通过双hash机制,一个hash记录使用频率和一个链表,一个hash记录key和node*,当查询时候,增加使用频率,从hash中的链表拿出,换到下一个使用频率hash的链表,时间复杂度为O(1),重要
- 需要维护一个minFreq的变量,用来记录LFU缓存中频率最小的元素,在缓存满的时候,可以快速定位到最小频繁的链表,以达到 O(1) 时间复杂度删除一个元素。 具体做法是:
- 更新/查找的时候,将元素频率+1,之后如果minFreq不在频率哈希表中了,说明频率哈希表中已经没有元素了,那么minFreq需要+1,否则minFreq不变。
- 插入的时候将minFreq改为1即可。
[!question] 缺点 一个数字一旦积累了次数就很难被替换下来,但是很多时候有的数据遇有时效性 而且消耗大量空间,因为所有出现过的key都要记录频率
[!quote] 场景 如果数据有明显的热点,即某些数据被频繁访问,而其他数据则很少被访问,那么 LFU 算法比较适合。例如,一个视频网站的首页,某些热门视频会被很多用户频繁地访问,而其他视频则很少被访问,这时 LFU 算法就能够更好地满足需求。
2. 两数相加
给你两个 **非空** 的链表,表示两个非负的整数。它们每位数字都是按照 **逆序** 的方式存储的,并且每个节点只能存储 **一位** 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
- 通过递归或者栈实现,注意进位
11. 盛最多水的容器
给定一个长度为 `n` 的整数数组 `height` 。有 `n` 条垂线,第 `i` 条线的两个端点是 `(i, 0)` 和 `(i, height[i])` 。
找出其中的两条线,使得它们与 `x` 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
**说明:**你不能倾斜容器。
- 典型双指针题目,每次移动短的边
class Solution {
public:
int maxArea(vector<int>& height) {
int begin=0,end=height.size()-1,result=0;
while (begin<end) {
result=max((end-begin)*min(height[end],height[begin]),result);
if (height[end]>height[begin]) {
begin++;
}else {
end--;
}
}
return result;
}
};
19. 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 `n` 个结点,并且返回链表的头结点。
- 典型双指针问题,一个指针先领先一个指针N个身位,然后后面到尾巴把前面先面的指针节点删除
23. 合并K个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
- 解法一
- 考虑两个链表的情况,典型的双指针
- 先1,2生成链表再依次和下一个合并
- 解法二
- 通过优先队列
32. 最长有效括号
给你一个只包含 `'('` 和 `')'` 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
- 看到括号上栈
class Solution {
public:
int longestValidParentheses(string s) {
int result=0,now=0;
stack<int> sta;
for (auto ch : s) {
if (ch==')') {
if (sta.empty()) {
now=0;
}else {
auto temp=sta.top();
sta.pop();
now+=2+temp;
result=max(result,now);
}
}else {
sta.push(now);
now=0;
}
}
return result;
}
};
33. 搜索旋转排序数组
整数数组 `nums` 按升序排列,数组中的值 **互不相同** 。
在传递给函数之前,`nums` 在预先未知的某个下标 `k`(`0 <= k < nums.length`)上进行了 **旋转**,使数组变为 `[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]`(下标 **从 0 开始** 计数)。例如, `[0,1,2,4,5,6,7]` 在下标 `3` 处经旋转后可能变为 `[4,5,6,7,0,1,2]` 。
给你 **旋转后** 的数组 `nums` 和一个整数 `target` ,如果 `nums` 中存在这个目标值 `target` ,则返回它的下标,否则返回 `-1` 。
你必须设计一个时间复杂度为 `O(log n)` 的算法解决此问题。
- 典型二分搜索变形题,当mid最小右边有序,mid最大左边有序,如果从小到大说明有序,有序部分直接二分搜索
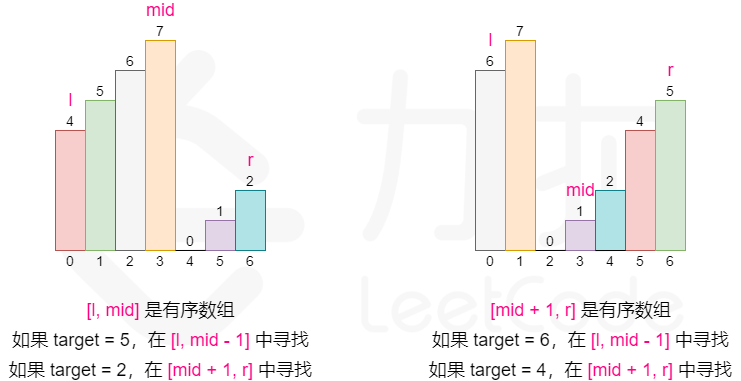
字节青训营考过
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 `nums`,和一个目标值 `target`。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 `target`,返回 `[-1, -1]`。
你必须设计并实现时间复杂度为 `O(log n)` 的算法解决此问题。
- 典型二分搜索
42. 接雨水
给定 `n` 个非负整数表示每个宽度为 `1` 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
- 单调栈
- 通过维持单调递减的栈,遇到大的就弹出并且计算储存的水数量
- 前缀数组
- 前缀和后缀,拿到交集

- 双指针
- 左右分别两个指针,小的指针移动,同时记录对应边的最高值计算雨水
56. 合并区间
以数组 `intervals` 表示若干个区间的集合,其中单个区间为 `intervals[i] = [starti, endi]` 。请你合并所有重叠的区间,并返回 _一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间_ 。
- 以左边界排序,排序之后,进行逐个比较右边界
84. 柱状图中最大的矩形
给定 _n_ 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
- 典型单调栈
- 在一维数组中对每一个数找到第一个比自己小的元素。这类“在一维数组中找第一个满足某种条件的数”的场景就是典型的单调栈应用场景。
155. 最小栈
设计一个支持 `push` ,`pop` ,`top` 操作,并能在常数时间内检索到最小元素的栈。
实现 `MinStack` 类:
- `MinStack()` 初始化堆栈对象。
- `void push(int val)` 将元素val推入堆栈。
- `void pop()` 删除堆栈顶部的元素。
- `int top()` 获取堆栈顶部的元素。
- `int getMin()` 获取堆栈中的最小元素。
- 辅助栈经典题目
对于栈来说,如果一个元素 a 在入栈时,栈里有其它的元素 b, c, d,那么无论这个栈在之后经历了什么操作,只要 a 在栈中,b, c, d 就一定在栈中,因为在 a 被弹出之前,b, c, d 不会被弹出。
因此,在操作过程中的任意一个时刻,只要栈顶的元素是 a,那么我们就可以确定栈里面现在的元素一定是 a, b, c, d。
那么,我们可以在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时,如果栈顶元素是 a,我们就可以直接返回存储的最小值 m。
946. 验证栈序列
给定 `pushed` 和 `popped` 两个序列,每个序列中的 **值都不重复**,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 `true`;否则,返回 `false` 。
- 纯粹的栈模拟,用一个栈模拟操作
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> st;
int n = pushed.size();
for (int i = 0, j = 0; i < n; i++) {
st.emplace(pushed[i]);
while (!st.empty() && st.top() == popped[j]) {
st.pop();
j++;
}
}
return st.empty();
}
};
- 若一个数字被pop,那么他右边到之前最大的数字之间的距离都应该被pop了
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
unordered_map<int, int> hashMap;
unordered_set<int> popnum;
for (int i = 0; i < pushed.size(); i++) {
hashMap.insert({pushed[i],i});
}
bool result=false;
int right=-1;
for (int i = 0; i < popped.size(); i++) {
auto temp=hashMap[popped[i]];
right=max(right,temp);
popnum.insert(temp);
if (right>temp) {
for (int i = temp+1; i < right; ++i) {
if (popnum.find(i)==popnum.end()) {
return false;
}
}
}
}
return true;
}
739. 每日温度
给定一个整数数组 `temperatures` ,表示每天的温度,返回一个数组 `answer` ,其中 `answer[i]` 是指对于第 `i` 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 `0` 来代替。
- 维护单调栈,经典题目
992. K 个不同整数的子数组
给定一个正整数数组 `nums`和一个整数 k ,返回 num 中 「**好子数组」** 的数目。
如果 `nums` 的某个子数组中不同整数的个数恰好为 `k`,则称 `nums` 的这个连续、不一定不同的子数组为 **「****好子数组 」**。
- 例如,`[1,2,3,1,2]` 中有 `3` 个不同的整数:`1`,`2`,以及 `3`。
**子数组** 是数组的 **连续** 部分。
- 三指针题目,恰好n个拆解为最多n个和最少n个的交集,成为三指针
- 左边为最长,中间为最短,右边负责移动
class Solution {
public:
int subarraysWithKDistinct(vector<int>& nums, int k) {
int left=0,mid=0,right=0,result=0;
unordered_map<int, int> hashMax,hashMin;
while (right!=nums.size()||left!=right) {
if (hashMax.size()==k) {
while (hashMin.size()!=k-1) {
hashMin[nums[mid]]--;
if (hashMin[nums[mid]]==0) {
hashMin.erase(nums[mid]);
}
mid++;
}
result+=mid-left;
if (right==nums.size()) {
break;
}
}
if (hashMax.size()<=k&&right!=nums.size()) {
hashMax[nums[right]]++;
hashMin[nums[right]]++;
right++;
}else if (hashMax.size()>=k&&left!=right) {
hashMax[nums[left]]--;
if (hashMax[nums[left]]==0) {
hashMax.erase(nums[left]);
}
left++;
}else {
break;
}
}
return result;
}
}
1944. 队列中可以看到的人数
有 `n` 个人排成一个队列,**从左到右** 编号为 `0` 到 `n - 1` 。给你以一个整数数组 `heights` ,每个整数 **互不相同**,`heights[i]` 表示第 `i` 个人的高度。
一个人能 **看到** 他右边另一个人的条件是这两人之间的所有人都比他们两人 **矮** 。更正式的,第 `i` 个人能看到第 `j` 个人的条件是 `i < j` 且 `min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1])` 。
请你返回一个长度为 `n` 的数组 `answer` ,其中 `answer[i]` 是第 `i` 个人在他右侧队列中能 **看到** 的 **人数** 。
- 单调栈,维护一个最大单调栈(反正右边小的会被忽略)
class Solution {
public:
vector<int> canSeePersonsCount(vector<int>& heights) {
reverse(heights.begin(),heights.end());
vector<int> result;
stack<int> sta;
for (int i = 0; i < heights.size(); i++) {
int now=heights[i];
int nowresult=0;
while (!sta.empty()&&heights[sta.top()]<now) {
sta.pop();
nowresult++;
}
if (!sta.empty()) {
nowresult++;
}
sta.push(i);
result.push_back(nowresult);
}
reverse(result.begin(), result.end());
return result;
}
};
402. 移掉 K 位数字
给你一个以字符串表示的非负整数 `num` 和一个整数 `k` ,移除这个数中的 `k` 位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。
- 使用单调栈,对于每个数字,如果该数字小于栈顶元素,我们就不断地弹出栈顶元素,直到
- 栈为空
- 或者新的栈顶元素不大于当前数字
- 或者我们已经删除了 k 位数字
- 如果做后k个数字还有剩余,就继续pop最后的数字
class Solution {
public:
string removeKdigits(string num, int k) {
vector<char> stk;
for (auto& digit: num) {
while (stk.size() > 0 && stk.back() > digit && k) {
stk.pop_back();
k -= 1;
}
stk.push_back(digit);
}
for (; k > 0; --k) {
stk.pop_back();
}
string ans = "";
bool isLeadingZero = true;
for (auto& digit: stk) {
if (isLeadingZero && digit == '0') {
continue;
}
isLeadingZero = false;
ans += digit;
}
return ans == "" ? "0" : ans;
}
}
2866. 美丽塔 II
给你一个长度为 `n` 下标从 **0** 开始的整数数组 `maxHeights` 。
你的任务是在坐标轴上建 `n` 座塔。第 `i` 座塔的下标为 `i` ,高度为 `heights[i]` 。
如果以下条件满足,我们称这些塔是 **美丽** 的:
1. `1 <= heights[i] <= maxHeights[i]`
2. `heights` 是一个 **山脉** 数组。
如果存在下标 `i` 满足以下条件,那么我们称数组 `heights` 是一个 **山脉** 数组:
- 对于所有 `0 < j <= i` ,都有 `heights[j - 1] <= heights[j]`
- 对于所有 `i <= k < n - 1` ,都有 `heights[k + 1] <= heights[k]`
请你返回满足 **美丽塔** 要求的方案中,**高度和的最大值** 。
- 有意思的单调栈题目,思路很难想,涉及到数组的区间替代的都是上单调栈,因为使用后面的替代前面的部分
class Solution {
public:
long long maximumSumOfHeights(vector<int> &maxHeights) {
stack<pair<long long, pair<long long, long long>>> sta;
vector<long long> prefix(maxHeights.size(), 0),
suffix(maxHeights.size(), 0);
for (int i = 0; i < maxHeights.size(); i++) {
while (!sta.empty() && sta.top().first > maxHeights[i]) {
sta.pop();
}
if (sta.empty()) {
sta.push({maxHeights[i], {(i + 1) * (long long)maxHeights[i], i}});
} else {
auto top = sta.top().second;
sta.push(
{maxHeights[i], {top.first + (long long)maxHeights[i] * (i - top.second), i}});
}
prefix[i] = sta.top().second.first;
}
while (!sta.empty()) {
sta.pop();
}
for (int i = maxHeights.size() - 1; i >= 0; i--) {
while (!sta.empty() && sta.top().first > maxHeights[i]) {
sta.pop();
}
if (sta.empty()) {
sta.push({maxHeights[i], {(maxHeights.size() - i) * (long long)maxHeights[i], i}});
} else {
auto top = sta.top().second;
sta.push(
{maxHeights[i], {top.first + (long long)maxHeights[i] * (top.second - i), i}});
}
suffix[i] = sta.top().second.first;
}
long long res = 0;
for (int i = 0; i < maxHeights.size(); i++) {
res = max(res, prefix[i] + suffix[i] - (long long)maxHeights[i]);
}
return res;
}
};