基本结构

  • 通常用 输入层,隐藏层,输出层 3个部分表示

隐藏层深度选择

  • 没有隐藏层：仅能够表示线性可分函数或决策
  • 隐藏层数=1：可以拟合任何“包含从一个有限空间到另一个有限空间的连续映射”的函数
  • 隐藏层数=2：搭配适当的激活函数可以表示任意精度的任意决策边界，并且可以拟合任何精度的任何平滑映射(基本两层就够了,两层基本相当于能够拟合任何函数了)
  • 隐藏层数>2：多出来的隐藏层可以学习复杂的描述(某种自动特征工程)
  • 层数越深，理论上拟合函数的能力增强，效果按理说会更好，但是实际上更深的层数可能会带来过拟合的问题，同时也会增加训练难度，使模型难以收敛。

神经元个数选择

  • 在隐藏层中使用太少的神经元将导致欠拟合(underfitting)。 相反，使用过多的神经元同样会导致一些问题。首先，隐藏层中的神经元过多可能会导致过拟合(overfitting)
  • 当神经网络具有过多的节点(过多的信息处理能力)时，训练集中包含的有限信息量不足以训练隐藏层中的所有神经元，因此就会导致过拟合。 即使训练数据包含的信息量足够，隐藏层中过多的神经元会增加训练时间，从而难以达到预期的效果。显然，选择一个合适的隐藏层神经元数量是至关重要的。

[!tip] 参考 如何确定神经网络的层数和隐藏层神经元数量？

梯度下降

202409923125952pasteboard.paste

  • 实际上就是通过根据倒数判断目前处在的位置应该向上还是向下继续行动, 根据对某个参数的偏导代表着这个参数的调整方向, 再和学习率相乘获得调整值

反向传播

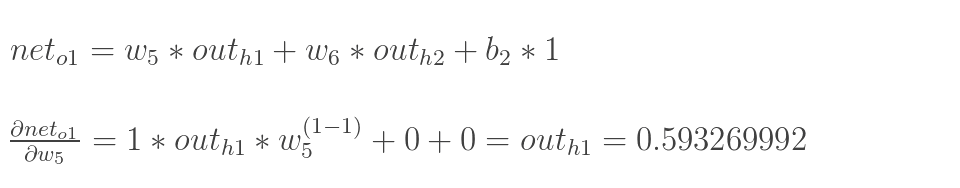
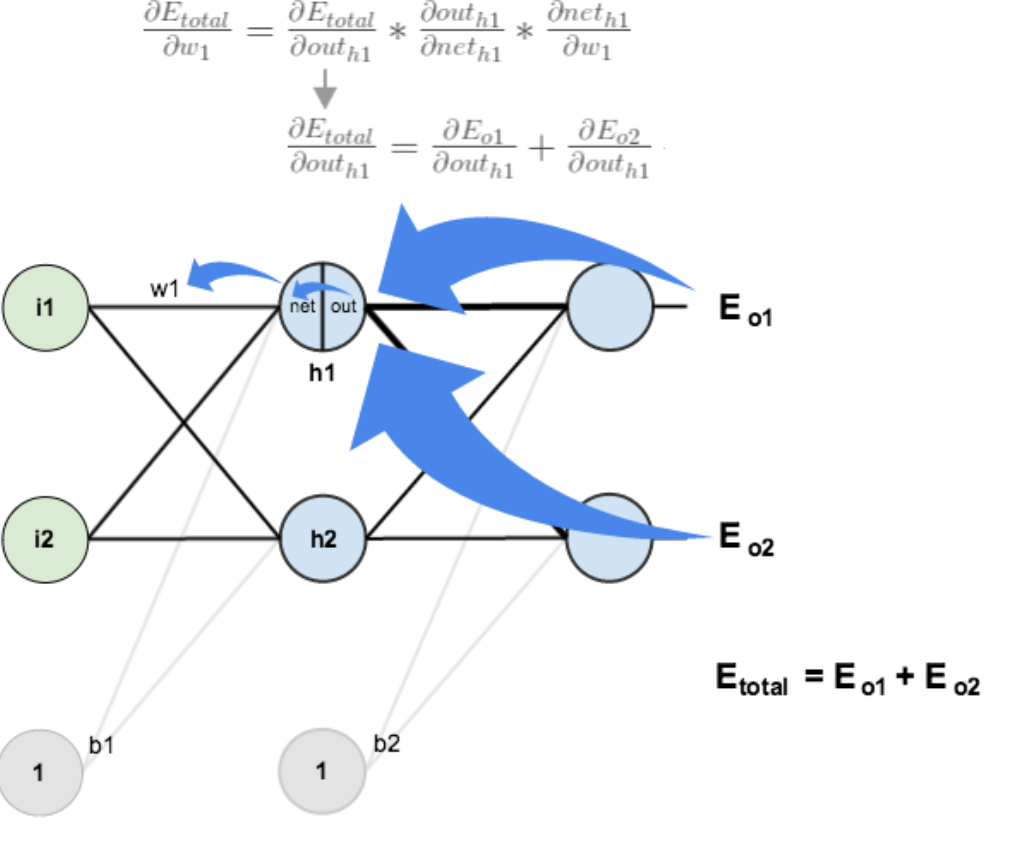
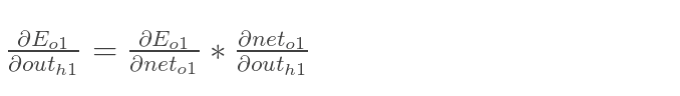
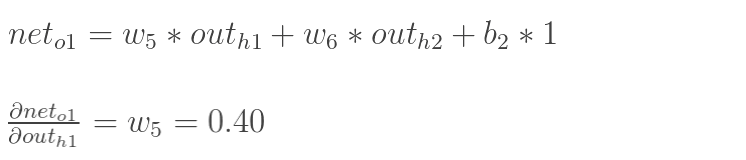
  • 实际上就是对某个变量进行求偏导 , 然后根据这个导数的值去调整这个变量的值, 调整的大小就是学习率
  • ∇C 作为 对变量 v 的偏导 ,C 作为代价函数 , 这个函数越小越好(这个函数可以变化的) $$C(w,b)\equiv\frac{1}{2n}\sum_{x}|y(x)-a|^{2}$$
  • ∆C ≈ ∇C · ∆v ∇C 把 v 的变化关联为 C 的变化，正如我 们期望的⽤梯度来表⽰。但是这个⽅程真正让我们兴奋的是它让我们看到了如何选取 ∆v 才能 让 ∆C 为负数。假设我们选取: ∆v = −η∇C
  • 这⾥的 η 是个很小的正数（称为学习速率）。 ∆C ≈ −η∇C·∇C = −η| ∇C |2。 由于 |∇C| 2 ≥ 0，这保证了 ∆C ≤ 0，如果我们按照⽅程的规则去改变 v，那么 C 会 ⼀直减小，不会增加。因此我 们把⽅程 (10) ⽤于定义球体在梯度下降算法下的“运动定律”。也就是说， 计 算 ∆v，来移动球体的位置 v： v → v ′ = v − η∇C 然后我们⽤它再次更新规则来计算下⼀次移动。如果我们反复持续这样做，我们将持续减小 C 直到 —— 正如我们希望的 —— 获得⼀个全局的最小值。
  • Sigmoid函数的求导结果为: $$ S′(x)=S(x)(1−S(x)) $$

[!tip] 参考 一文弄懂神经网络中的反向传播法——BackPropagation - Charlotte77 - 博客园

Softmax回归

  • 实际上就是将最终的输出进行归一化处理, 使其可以直接进行交叉熵的计算

拟合问题

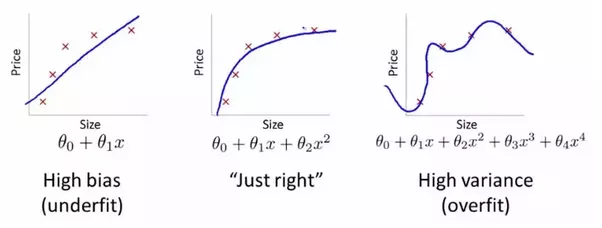
  • 当出现训练数据损失不停减少, 但是测试数据损失在增加的时候. 说明出现了过拟合的问题

出现问题

训练不拟合

  • 很多可能的原因,比如数据太垃圾, 或者学习率太大了 ,或者数据不够, 或者网络太渣了

神经元停止学习

代码参考

[!tip] 参考

入门推荐书籍📚

[!tip] 最推荐的两本书 Neural networks and deep learning 中文版是 GitHub - zhanggyb/nndl: Another Chinese Translation of Neural Networks and Deep Learning 《图解深度学习：可视化、交互式的人工智能指南》(乔恩·克罗恩（Jon Krohn）)【简介_书评_在线阅读】 - 当当图书

GPT 原理

参数

  • 每个 token 都变成一个向量 , 每个向量维度有 12288 维度

上下文输入

  • 输入的 context size 为 2048 ,意味着上下文输入的 token 最大值为 2048个, 这就是为什么大模型遗忘的原因

Temperature

  • 就是在输出层输出的时候 , 这个数字越大就意味着输出越平均 , 越可能选择不确定的选项(更有创造性输出)